|
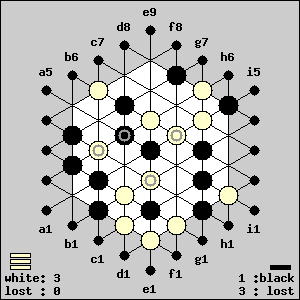
Solution 5 (Online GIPF Puzzle Contest) 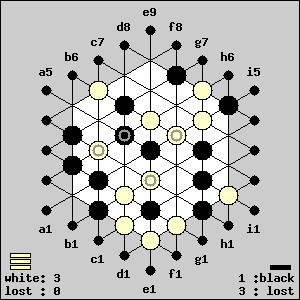 White: b6-g4 A complex situation. White cannot prevent Black
from recycling pieces. If he prevents it on the a3-g1 line, he'll
always create another possibility.
The GIPF-piece on f5
doesn't look dangerous yet, but it will become a threat... with
Black's help.
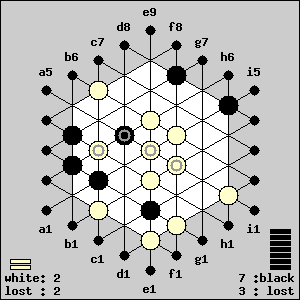
If i5-d4 and b1-f4 would have been
played in reversed order, the result would have been exactly the
same. It also makes no difference whether Black captures on the
a3-g1 line or on the d1-d8 line. If he chooses xd2,d3,d4,d6,
he would leave himself 2...a2-f6 to push his GIPF away
from the dangerous d5-spot, but the white piece on f2
makes that escape impossible. So, the only thing Black can do
to postpone losing his GIPF-piece (no matter which row he removed),
is pushing the piece on h2 towards g2 or h3.
But that postpones it just with one move: White occupies g3
with his third move and captures Black's GIPF with his fourth
move. White wins with 4 moves, which is the shortest way! |